Trong chương trình toán lớp 6 các bạn học sinh được làm quen với một thuật ngữ mới đó là: “Phần tử”. Vậy phần tử là gì? Phần tử của tập hợp là gì? Công thức tính phần tử của tập hợp như thế nào? Mời quý phụ huynh và các em học sinh tham khảo bài viết sau của chúng tôi.

1. Phần tử của tập hợp là gì?
a. Khái niệm phần tử của tập hợp.
- Một tập hợp có thể có một phần tử, có nhiều phần tử, có vô số phần tử hoặc cũng có thể không có phần tử nào.
Ví dụ 1: A là tập hợp các số tự nhiên nhỏ hơn 4
Các số 0,1,2,3 là các phần tử của tập hợp
Kí hiệu:
1 ∈ A
đọc là 1 thuộc A hoặc 1 là phần tử của A
5 ∉ A
đọc là 5 không thuộc A hoặc 5 không là phần tử của A.
Ví dụ 2: Tập hợp các số tự nhiên là tập hợp có vô số phần tử.
– Tập hợp không có phần tử nào gọi là tập rỗng. Tập rỗng kí hiệu là Ø.
b. Cách viết một tập hợp.
Để viết 1 tập hợp, thường có 2 cách:
+ Liệt kê các phân tử của tập hợp
Ví dụ,
A = { 0; 1; 2; 3; 4},
B = { a; b; c}
+ Chỉ ra tính chất đặc trưng cho tập hợp
A = { x ∈ N | x < 5 }, N là tập hợp các số tự nhiên
Tính chất đặc trưng cho các phần tử x của tập hợp A đó là
x ∈ N và x < 5
Lưu ý:
- Các phần tử được viết trong dấu { }.
- Các phần tử được liệt kê một lần không kể thứ tự liệt kê
- Các phần tử cách nhau bởi dấu “;”
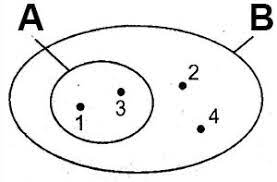
Minh họa tập hợp bằng 1 vòng kín được gọi là biểu đồ ven.

c. Một số tập hợp thường gặp.
– Tập hợp số tự nhiên
Kí hiệu N:
N = { 0; 1; 2; 3; 4…}
– Tập hợp số tự nhiên khác 0
Kí hiệu
N∗ = {1; 2; 3; 4…}
– Tập hợp rỗng
Tập hợp số tự nhiên sao cho x+10=8 là tập hợp rỗng ( không có x thỏa mãn)
Tập hợp rỗng kí hiệu là ∅
Lưu ý: một tập hợp có thể có 1 phần tử, nhiều phần tử, vô số phần tử (tập hợp số tự nhiên N) hoặc không có phần tử nào (tập hợp rỗng)
2. Cách cho một tập hợp.
Có 2 cách cho một tập hợp:
Cách 1: Liệt kê các phần tử của tập hợp
Ví dụ: B = {0; 2; 4; 6; 8}
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp
Ví dụ: B = {x | x là số tự nhiên chẵn, x < 10}
3. Một số bài tập về tập hợp.
Bài 1: Cho hai tập hợp A = {1; 2; 3} và B = {4; 5}
a) Hãy viết tập hợp C gồm một phần tử thuộc A và một phần tử thuộc B. Có bao nhiêu tập hợp như vậy?
Trả lời:
Tập hợp C có hai phần tử: 1 phần tử thuộc A và 1 phần tử thuộc B. Do đó có tất cả 3 x 2 = 6 tập hợp thỏa mãn. Đó là: {1; 4}, {1; 5}, {2; 4}, {2; 5}, {3; 4}, {3; 5}
b) Hãy viết tập hợp D gồm một phần tử thuộc A và hai phần tử thuộc B. Có bao nhiêu tập hợp như vậy?
Trả lời:
Tập hợp D có ba phần tử: một phần tử thuộc A và hai phần tử thuộc B. Do đó có tất cả 3 x 1 = 3 tập hợp thỏa mãn. Đó là: {1; 4; 5}, {2; 4; 5}, {3; 4; 5}.
Bài 2: Hãy tính số phần tử của tập hợp A gồm các số tự nhiên chẵn liên tiếp từ 1990 đến 3000.
Trả lời:
Các số tự nhiên chẵn liên tiếp từ 1990 đến 3000 hơn kém nhau 2 đơn vị. Do đó số phần tử của tập hợp A là: (3000 – 1990) : 2 + 1 = 506 phần tử.
Bài 3: Hãy tính số phần tử của tập hợp: B = { x “thuộc” N* | x = 3k và 1000 < x < 3000}
Trả lời:
Cách 1: Phần tử nhỏ nhất của B là 1002 ứng với k = 334. Phần tử lớn nhất của B là 2997 ứng với k = 999. Vậy số phần tử của B là (999 – 334) : 1 + 1 = 666 phần tử.
Cách 2: Tập hợp B gồm các phần tử là các số tự nhiên chia hết cho 3 từ 1002 đến 2997. Hai phần tử liên tiếp của B hơn kém nhau 3 đơn vị, nên số phần tử của B là: (2997 – 1002) : 3 + 1 = 666 phần tử.
Bài 4: Cho tập hợp A = {Nho; Mận; Hồng; Đào}. Hãy viết tất cả các tập hợp con có 3 phần tử của A.
Trả lời:
Các tập hợp con có 3 phần tử của A là: {Nho; Mận; Hồng}, {Nho; Mận; Đào}, {Mận; Hồng; Đào}, {Nho; Hồng; Đào}.
Phần tử của tập hợp là một dạng toán tương đối khó với các em học sinh. Hãy tham khảo bài viết của chúng tôi và vận dụng nó để làm bài tập các em nhé.
>>> Xem thêm:
