
Trong thời gian gần đây https://vietnamblackberry.vn/ nhận được rất nhiều câu hỏi từ phía độc giả gửi về cho chúng tôi với nội dung “Số thực là gì? Số thực gồm những số nào? Số 0 có phải số thực?” Ngày hôm nay, chúng tôi sẽ giải đáp thắc mắc đó cho quý độc giả thông qua bài viết sau đây. Mời quý độc giả cùng đón đọc.

1. Số thực là gì? Tính chất và thuộc tính của số thực.
a. Số thực là gì?
- Số thực, tiếng Anh là Real numbers là tập hợp bao gồm số dương (1,2,3), số 0, số âm (-1,-2,-3), số hữu tỉ (5/2, -23/45), số vô tỉ (số pi, số √ 2).
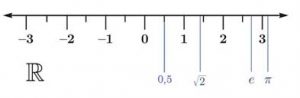
- Số thực có thể được xem là các điểm nằm trên trục số dài vô hạn.
- Hiểu một cách đơn giản hơn thì số thực là tập hợp các số hữu tỉ và vô tỉ.
- Tập hợp số thực kí hiệu là R (R = Q U I).
- Một số thực có thể là số đại số hoặc số siêu việt. Ta cũng có số thực âm (-1, -3/4…) và số thực dương (5, 7, √ 2…).
- Số tự nhiên, số nguyên, số hữu tỉ và số vô tỷ đều thuộc tập hợp số thực. Đây là tập hợp số lớn nhất và được coi là một hệ thống đại số đồ sộ. Ngoại trừ số 0 nằm ở vị trí trung tâm của trục số, bất kì số thực khác sẽ đều có thể là số âm hoặc số dương. Bản chất của R cũng như các tập con khác, đều là các tập hợp số vô hạn. Tuy nhiên quy mô của tập hợp này quá lớn khiến số lượng số thực là không đếm được.
- Khái niệm số thực lần đầu tiên được sử dụng vào thế kỷ 17 bởi nhà toán học người Pháp René Descartes để biểu thị các giá trị nghiệm của đa thức và phân biệt với các nghiệm ảo. Tuy nhiên, đến tận năm 1871 khái niệm chính xác nhất và được sử dụng cho tới tận ngày nay về số thực mới được công bố bởi nhà toán học Georg Cantor.
b. Tính chất của số thực.
Số thực có các tính chất sau đây:
- Bất kỳ số thực nào khác 0 thì sẽ là số âm hoặc số dương.
- Tổng hay tích của hai số thực không âm là một số thực không âm.
- Số thực là tập hợp vô hạn các số vô cùng nhiều không đếm được các số thực.
- Số thực có hệ thống các tập hợp con vô hạn có thể đếm được.
- Số thực có thể biểu thị bằng biểu diễn thập phân.
- Số thực có thể được sử dụng để thể hiện các phép đo đại lượng liên tục.
c. Thuộc tính của số thực.
Các thuộc tính của số thực là:
- Thuộc tính trường có thứ tự
Thuộc tính này chỉ rằng các số thực bao gồm một trường, với phép cộng và phép nhân cùng với phép chia cho các số khác không. Chúng có thể được sắp xếp hoàn toàn trên một trục số hoành theo cách tương thích với phép cộng và phép nhân.
- Thuộc tính cận trên thấp nhất
Thuộc tính này chỉ ra rằng nếu tập hợp một số thực không trống có giới hạn trên thì nó có cận trên chính là những số thực nhỏ nhất.
2. Số thực gồm những số nào?
a. Số thực gồm những số nào?
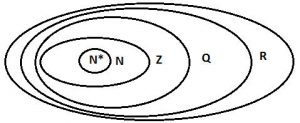
Số thực gồm:
- Số tự nhiên N: N = {0, 1, 2, 3…}
- Số nguyên Z: Z = {…-3, -2, -1, 0, 1, 2, 3…}
- Số hữu tỉ Q: Q = {x = a/b; trong đó a,b ϵ Z, và b ≠0}
- Số vô tỉ I: I ={thập phân vô hạn không tuần hoàn, ví dụ căn bậc 2}
b. Trục số thực?
- Mỗi số thực được biểu diễn bởi một điểm trên trục số.
- Ngược lại mỗi điểm trên trục số đều biểu diễn một số thực.
- Chỉ có tập hợp số thực mới lấp đầy trục số.
Chú ý: Các phép toán trong tập hợp các số thực cũng có các tính chất tương tự như các phép toán trong tập hợp số hữu tỉ. Ta có Z ⊂ Q ⊂ R.
Chúng ta được biết, Tập hợp số thực được đặt làm đối trọng với tập hợp số phức. Trong đó, số phức còn được gọi là số ảo, tức không thể biểu diễn trên trục số, cũng như có nhiều phương trình và bài toán không thể giải được trong trường số phức. Ví dụ như (x + 1) = -9, hay như phép tính √ -1 (căn bậc hai của -1 và các số âm khác).
3. Một số bài tập về số thực.
Bài 1: Điền các dấu ∈, ∉, ⊂ thích hợp vào chỗ trống (…) sao cho đúng:
- 5 …. Q ; 5 …. R ; 5… I ; -2,53… Q
- 0,2(35) …. I ; N …. Z ; I …. R
Giải:
- 5 ∈ Q ; 5 ∈ R ; 5 ∉ I ; -2,53∈ Q
- 0,2(35) ∉ I ; N ∈ Z ; I ⊂ R
Bài 2: Cho các số thực: -3,2 ; 1 ; -1/2 ; -7,4 ; 0 ; -1,5. Hãy sắp xếp:
a) Theo thứ tự từ nhỏ đến lớn.
b) Theo thứ tự từ bé đến lớn theo giá trị tuyệt đối của chúng.
Giải.
a)Sắp xếp theo thứ tự như sau: – 3,2 < -1,5 < -1/2 < 0 < 1 < 7,4.
b) 0 < 1/2 < 1 < 1,5 < 3,2 < 7,4.
Vì vậy:
|0| < |-1/2| < |1| < |-1,5| < |-3,2| < |7,4|.
Bài 3: Tìm x, biết: 3,2.x + (-1,2).x +2,7 = -4,9 ;
Giải.
3,2. x + (-1,2).x + 2,7 = -4,9
[3,2 + (-1,2)].x + 2,7 = -4,9.
2.x + 2,7 = – 4,9.
2.x = – 4,9 – 2,7
2.x = – 7,6
x = -7,6 : 2
x = -3,8
Trên đây là những kiến thức về số thực mà chúng tôi tổng hợp được. Hi vọng, qua bài viết này quý độc giả sẽ có thêm nhiều kiến thức từ đó vận dụng linh hoạt để làm bài tập. Xin cảm ơn.
>>> Xem thêm:
