Trong hình học chắc hẳn các bạn đã nghe tới khái niệm tia phân giác của một góc đúng không ạ. Vậy tia phân giác của một góc là gì? Tính chất của tia phân giác của một góc ra sao? Kính mời quý phụ huynh và các em học sinh tham khảo bài viết sau của chúng tôi để có câu trả lời nhé.
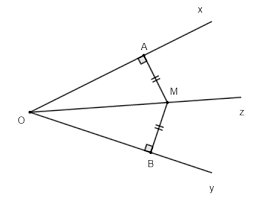
1. Tia phân giác của một góc.
a. Khái niệm tia phân giác của một góc.
Tia phân giác của một góc trong toán học được xác định tương đối rõ. Là tia nằm ở giữa hai cạnh của một góc và được chia góc đó thành hai góc bằng nhau.
Ví dụ: Ta có một góc xOy. Nếu tia On nằm ở giữa hai tia Ox và Oy cùng chia góc xOy thành hai góc bằng nhau, thì tia On sẽ được gọi là tia phân giác của một góc xOy.
b. Dấu hiệu nhận biết tia phân giác của một góc.
+ Tia chia một góc thành 2 góc bằng nhau và có số đo bằng nửa số đo của góc đã cho là tia phân giác của góc đó.
+ Tia sẽ nằm trong một góc và ở một điểm trên nó cách đều của hai tia tạo thành góc là tia phân giác của một góc.
c. Tính chất tia phân giác của một góc.
+ Tia phân giác của một góc sẽ có hai tính chất tương đối là quan trọng mà bạn đọc cần nắm được. Chi tiết cụ thể bao gồm:
+ Tia phân giác của một góc được chia góc đó thành hai góc nhỏ hơn có số đo bằng nhau và bằng một nửa của góc ban đầu.
+ Tất cả các điểm trên tia phân giác của một góc sẽ cách đều hai tia tạo thành góc.
2. Bài tập vận dụng về tia phân giác.
a. Chứng minh một tia phân giác của một góc cho trước.
Phương pháp giải: Chứng minh tia Oy là tia phân giác của góc xOz
+ Cách 1. Chứng minh tia Oy nằm giữa hai tia Ox và Oz
Chứng minh góc xOy = góc yOz
+ Cách 2: Chứng minh góc xOy = góc yOz = 1/2 góc xOz
+ Cách 3: Dùng tính chất đường trung tuyến trong tam giác cân đồng thời là đường phân giác
Bài 1. Cho tam giác ABC, hai đường phân giác của hai góc ngoài đỉnh B và đỉnh C cắt nhau tại E. Chứng minh E thuộc phân giác trong của BAC.
Bài làm.
Từ E hạ EH vuông góc BC, EF vuông góc AB, EG vuông góc AC với H thuộc BC, F thuộc AB, G thuộc AC.
Ta có:
EF = EH (E thuộc phân giác ngoài của góc B) (1)
và EH = EG (E thuộc phân giác ngoài của góc C) (2)
Từ (1) và (2) ta có: EF = EG => E thuộc tia phân giác trong của góc BAC (tính chất tia phân giác của một góc).
Bài 2. Cho tam giác ABC vuông tại A . Từ một điểm K bất kì trên cạnh BC, kẻ KH vuông góc AC (H thuộc AC). Trên tia đối của tuan HK lấy điểm I sao cho HI = HK. Chứng minh:
a. AB // HK
b. góc KAH = góc IAH
c. tam giác AKI cân
Bài làm.
a. Ta có: AB vuông góc AC (tam giác ABC vuông tại A),
KH vuông góc AC (giả thiết)
=> AB // KH (từ vuông góc đến song song)
b. Xét tam giác AHK và tam giác AHI, có:
Hk = HI (giả thiết)
góc AHK = góc AHI = 90 (giả thiết)
AH chung
Do đó, tam giác AHK = tam giác AHI (hai cạnh góc vuông)
=> góc KAH = góc IAh (hai góc tương ứng)
c. Theo câu b, ta có: tam giác AHK = tam giác AHI => AK = AI (hai cạnh tương ứng)
=> tam giác AKI cân tại A.
b. Dạng 2. Tính số đo góc.
Bài 1. Cho hai góc xOy và góc yOz là hai góc kề bù, biết góc xOy = 120
a. Tính góc yOz
b. Gọi Om là tia phân giác của góc xOy. Tính góc zOm
Bài làm
a. Vì góc xOy và góc yOz là hai góc kề bù nên ta có góc xOy + góc yOz = 180 hay góc yOz = 180 – góc xOy = 60
b. Tia Om là tia phân giác của góc xOy nên góc xOm = mOy = góc xOy / 2 = 120/2 = 60
Hai góc xOm và zOm kề bù nên góc xOm + góc zOm = 180
=> góc zOm = 120
c. Dạng 3. Vận dụng tính chất của một góc để chứng minh các đoạn thẳng bằng nhau.
Phương pháp giải: Áp dụng định lí thuận: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Bài 1. Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt đường thẳng vuông góc với BC tại trung điểm của BC ở D. Gọi H và K là chân các đường vuông góc kẻ từ D đến các đường thẳng AB, AC. Chứng minh: BH = CK.
Bài làm
TA có: D thuộc phân giác của góc A
DH vuông góc với AB, DK vuông góc với AC
=> DH = DK (tính chất tia phân giác của một góc)
Gọi G là trung điểm của BC
Xét tam giác BGD và tam giác CGD, ta có:
góc BGD = góc CGD = 90° (DG là đường trung trực của BC)
BG = CG (giả thiết)
DG là cạnh chung
Do đó, tam giác BGD = tam giác CGD (hai cạnh góc vuông)
=> BD = CD (hai cạnh tương ứng)
Xét tam giác BHD và tam giác CKD có:
góc BHD = CKD = 90°
DH = DK (chứng minh trên)
BD = CD (chứng minh trên)
Do đó, tam giác BHD = tam giác CKD (cạnh huyền – cạnh góc vuông)
=> BH = CK (hai cạnh tương ứng).
Trên đây là kiến thức về tia phân giác của một góc mà chúng tôi tổng hợp được. Hi vọng qua bài viết này các em học sinh sẽ nắm được kiến thức về tia phân giác qua đó vận dụng vào làm bài tập.
>>Xem thêm:
