Hình thang là gì? Khái niệm, tính chất, dấu hiệu nhận biết. Công thức tính chu vi và diện tích hình thang thường, vuông, cân. Các dạng bài tập minh hoạ.
1.Hình thang là gì?
a. Khái niệm.
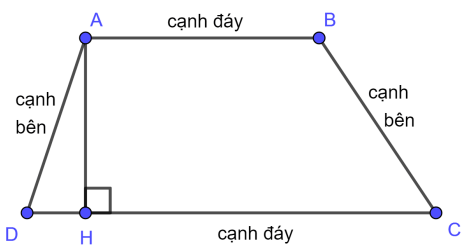
- Hình thang trong hình học là một tứ giác có hai cạnh đối song song. Hai cạnh song song này được gọi là các cạnh đáy của hình thang, hai cạnh còn lại gọi là cạnh bên.
- Hình thang là tứ giác có hai cạnh đối song song, hai góc kề một cạnh bên có tổng bằng 180 độ.
- Hình thang là tứ giác lồi có 4 cạnh. Trong đó có hai cạnh song song với nhau được gọi là cạnh đáy, hai cạnh còn lại được gọi là hai cạnh bên.
Có 3 loại hình thang thường gặp là:
- Hình thang thường
- Hình thang vuông
- Hình thang cân
b. Tính chất của hình thang.
- Tính chất về cạnh:
+ Hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên sẽ song song và bằng nhau.
+ Hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau.
- Đường trung bình của hình thang:
+ Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang
+ Tính chất: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
- Tính chất về góc:
+ Hai góc kề một cạnh bên của hình thang có tổng bằng 180 độ ( Hai hóc nằm ở vị trí trong cùng của hai đoạn thẳng song song là hai cạnh đáy) .
+ Trong hình thang cân, hai góc kề một đáy bằng nhau.
c. Dấu hiệu nhận biết.
+ Hình thang là hình tứ giác có hai cạnh đối song song với nhau.
+ Tứ giác là hình thang có một góc vuông là hình thang vuông.
+ Tứ giác là hình thang có hai góc kề 1 cạnh đáy bằng nhau thì là hình thang cân.
+ Tứ giác là hình thang có hai cạnh bên hình thang bằng nhau thì là hình thang cân.
+ Tứ giác là hình thang mà hai đường chéo của chúng bằng nhau thì là hình thang cân.
2. Công thức tính chu vi hình thang.
P = a + b + c + d
Trong đó: P là chu vi hình thang,
a và b lần lượt là độ dài 2 cạnh đáy,
c và d lần lượt là độ dài 2 cạnh bên.
Ví dụ minh họa:
Một hình thang có độ dài các cạnh bên lần lượt là 4cm, độ dài đáy lớn là 8 cm và độ dài đáy bé là 4 cm. Tính chu vi hình thang.
Bài giải:
Chu vi hình thang là:
4+4+4+8 = 20 (cm)
Đáp số chu vi của hình thang = 20 cm
3. Công thức tính diện tích hình thang.
Bài thơ về tính diện tích hình thang khá dễ nhớ như sau:
Muốn tính diện tích hình thang
Đáy lớn đáy nhỏ ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra
Công thức:
S = (a + b)/2 x h
Trong đó:
S là diện tích hình thang.
a và b là độ dài 2 cạnh đáy.
h là chiều cao hạ từ cạnh đáy a xuống b hoặc ngược lại (khoảng cách giữa 2 cạnh đáy).
4. Một số dạng bài tập về hình thang.
a. Tính diện tích hình bình thang khi biết độ dài hai đáy và chiều cao
Ví dụ: Cho hình thang có độ dài đáy nhỏ bằng 3cm, đáy lớn bằng 5cm. Chiều cao của hình thang bằng 4cm. Tính diện tích của hình thang đó.
Lời giải:
Diện tích hình thang là:
(3 + 5) x 4 : 2 = 16 (cm2)
Đáp số: 16cm2
Tính chiều cao khi biết độ dài hai đáy và diện tích.
Ví dụ: Một hình thang vuông có diện tích bằng 7dm2, đáy bé bằng 2dm và đáy lớn bằng 5dm. Tính độ dài chiều cao của hình thang vuông đó.
Từ công thức tính diện tích hình thang, ta suy ra được công thức tính chiều cao của hình thang, đó là: h = S x 2 : (a + b) (Để tính chiều cao của hình thang, ta lấy diện tích chia cho trung bình cộng của hai đáy.)
Lời giải:
Độ dài chiều cao của hình thang là:
7 x 2 : (2 + 5) = 2 (dm)
Đáp số: 2dm
Trên đây là một số thông tin về hình thang, khái niệm, tính chất, dấu hiệu nhận biết…công thức tính chu vi, diện tích hình thang, một số bài tập minh hoạ.
