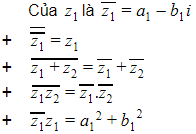Như các bạn đã biết thì số phức là một trong những phần kiến thức rất quan trọng trong chương trình đại số lớp 12. Trong các bài kiểm tra hay thi khảo sát chúng ta rất hay bắt gặp dạng toán này. Để tìm hiểu rõ hơn về số phức https://vietnamblackberry.vn/ sẽ giới thiệu đến các bạn bài viết “Số phức là gì? Các công thức số phức 12 và bài tập minh họa.” Hãy tham khảo ngay bài viết của chúng tôi để tìm hiểu rõ hơn về số phức nhé.

1. Số phức là gì?
a. Khái niệm số phức.
- Số phức (dạng đại số) sẽ có dạng: z = a + bi , trong đó a, b là các số nguyên, a được gọi là phần thực, b được gọi là phần ảo. Và i được xem là đơn vị ảo, qui ước i2 = -1
- Tập hợp số phức được kí hiệu là C.
- Nếu z là số thực thì phần ảo b = 0, ngược lại, nếu z là số thuần ảo thì phần thực của z là a = 0.
- Xét hai số phức z = a + bi và z’ = a’ + b’i , đối với số phức, ta chỉ xét xem hai số phức có bằng nhau hay không. Điều kiện 2 số phức bằng nhau z = z’ khi và chỉ khi a = a’, b = b’ .
b. Biểu diễn hình học của số phức.
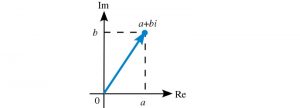
- Cho số phức z = a + bi (a,b nguyên). Xét trong mặt phẳng phức Oxy, z sẽ được biểu diễn bởi điểm M(a;b) hoặc bởi vector u = (a;b). Chú ý ở mặt phẳng phức, trục Ox còn được gọi là trục thực, trục Oy gọi là trục ảo.
c. Các phép tính trong số phức.
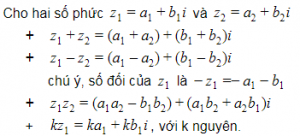
d. Modun của số phức.
- Có thể hiểu modun của số phức z = a+bi là độ dài của vector u (a,b) biểu diễn số phức đó.
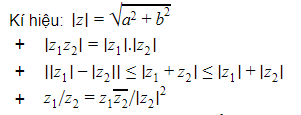
e. Số phức liên hợp.
2. Một số bài tập minh họa.
Bài tập 1: Tìm giá trị của m để phương trình sau z + mz + i = 0 có hai nghiệm z1 , z2 thỏa đẳng thức z12 + z2 2 = -4i.
Bài làm
Chú ý, đối với phương trình bậc 2 thì hệ thức Vi-et về nghiệm luôn được sử dụng. Như vậy ta có: z1 + z2 = -m, z1z2 = i.
Theo đề bài:
z12 + z2 2 = -4i
=> (z1 + z2)2 – 2z1z2 = -4i
=> m2 = -2i.
Đến đây, bài toán qui về tìm căn bậc hai cho 1 số phức. Áp dụng phần kiến thức đã nêu ở trên, ta giải hệ sau: gọi m=a+bi, suy ra ta có hệ:
a2 + b2 = 0, 2ab = -2i
=> (a,b) = (1,-1) hoặc (a,b) = (-1,1).
Vậy có hai giá trị của m thỏa mãn đề bài.
Bài tập 2 : Tìm các số thực x, y sao cho đẳng thức sau là đúng:
a) 5x + y + 5xi = 2y – 1 + (x-y)i
b) (-3x + 2y)i + (2x – 3y + 1)=(2x + 6y – 3) + (6x – 2y)i
Bài làm
a) Ta xem xét mỗi vế là một số phức, như vậy điều kiện để 2 số phức bằng nhau là phần thực bằng phần thực, phần ảo bằng phần ảo.
Ta có: 5x + y = 2y – 1; 5x = x – y, suy ra x = -1/7; y = 4/7
b) Câu này tương tự câu trên, các bạn cứ việc đồng nhất phần thực bằng phần thực, phần ảo bằng phần ảo là sẽ tìm ra được đáp án.
Bài tập 3: Tìm số phức biết:
a) |z| = 5 và z = z
b) |z| = 8 và phần thực của z bằng 5 lần phần ảo của z.
Bài làm
a) Giả sử z = a + bi, suy ra z = a – bi . Khi đó:
a2 + b2 = 52; a = a; b = -b (do z = z)
suy ra b = 0, a = 5
Vậy có 2 số phức z thỏa đề bài là z = 5 và z = -5
b) Hướng đi là lập hệ phương trình bậc nhất hai ẩn, từ đó giải tìm ra được phần thực và phần ảo của z.
Như vậy, cách để giải quyết dạng này là dựa vào các tính chất của số phức, ta lập các hệ phương trình để giải, tìm ra phần thực và ảo của số phức đề bài yêu cầu.
Hi vọng với những kiến thức mà chúng tôi tổng hợp tổng hợp được sẽ giúp ích cho các em học sinh. Hãy luyện tập thật nhiều để thành thạo hơn về dạng này nhé.
>> xem thêm.