Trong cuộc sống hằng ngày ta gặp rất nhiều đồ vật có hình khối trụ đúng không nhỉ? Các bạn muốn tính diện tích hay thể tích các hình khối trụ đó mà chưa biết cách làm ra sao hãy tham khảo ngay ngay bài viết của https://vietnamblackberry.vn/ nhé.
1. Hình trụ là gì?
a. Khái niệm.
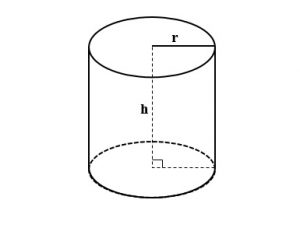
- Hình trụ là một hình học không gian (3D), là hình được giới hạn bởi hai đường tròn có đường kính bằng nhau và mặt trụ.
Theo định nghĩa sách giáo khoa Toán lớp 9, hình trụ là là:
- “Hình trụ là hình giới bạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ và 2 mặt phẳng vuông góc với trục.”
- “Hình trụ là hình tròn xoay khi sinh bởi bốn cạnh của hình một hình chữ nhật khi quay xung quanh một đường trung bình của hình chữ nhật đó.”
Theo một cách dễ hiểu hơn, ta sẽ có một hình trụ khi xoay một hình chữ nhật ABCD theo một cạnh cố định.
b. Dấu hiệu nhận biết hình khối trụ.
Để có thể nhận biết hình trụ một cách dễ dàng, bạn có thể dựa vào một số tính chất sau:
- Hình trụ có hai mặt đáy là hình tròn và đường kính bằng nhau
- Hai cạnh có độ dài bằng nhau khi chúng song song với nhau
- Đường thẳng nối từ hai tâm của hai mặt đáy chính là trục tọa độ của hình trụ.
- Các đường thẳng có cùng độ dài và song song với trục tọa độ được gọi là các đường sinh của hình trụ.
2. Công thức tính diện tích hình trụ.
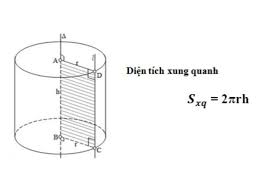
a. Công thức tính diện tích xung quanh hình trụ.
- Khái niệm.
+ Diện tích hình trụ được hiểu là toàn bộ không gian chiếm giữ bằng cách tính tổng diện tích xung quanh và diện tích hai đáy. Bên cạnh đó, diện tích toàn phần hình trụ sẽ là diện tích của mặt xung quanh hình trụ không bao gồm diện tích hai đáy.
+ Ta xét đến diện tích xung quanh hình trụ tròn chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ tròn và không gồm diện tích hai đáy.
- Công thức tính diện tích xung quanh.
+ Công thức tính diện tích xung quanh hình trụ bằng chu vi đường tròn đáy nhân với chiều cao:
Sxung quanh = 2 x π x r x h
Trong đó:
+ r được hiểu là bán kính hình trụ.
+ h chính là chiều cao nối từ đáy tới đỉnh trụ.
b. Công thức tính diện tích toàn phần hình trụ.
+ Diện tích toàn phần của hình trụ bao gồm phần diện tích bao quanh và diện tích đáy của hình trụ.
+ Để tính được diện tích toàn phần hình trụ, chúng ta sẽ lấy diện tích xung quanh hình trụ cộng với diện tích của 2 đáy.
Công thức cụ thể là:
STP = 2.Π.R² + 2.Π.R.H
Trong đó:
+ Stp là diện tích toàn phần hình đáy
+ 2πr^2 diện tích của 2 đường tròn đáy (với π = 3,14)
+ 2πrh là diện tích xung quanh hình đáy
3. Một số bài tập về tính diện tích hình trụ.
Bài tập 1: Cho một hình trụ có r = 5 cm, h = 10 cm. Hãy tính diện tích xung quanh và diện tích toàn phần của hình trụ.
Bài làm
Diện tích xung quanh hình trụ là:
Sxq = 2 * π * r * h = 2 * π * 5 * 10 = ~ 314 (cm2)
Diện tích toàn phần hình trụ là:
Stp = 2 * π * r ^2* + Sxq = 2 * π * 5^2 + 314= ~ 471 cm2
Bài tập 2: Yêu cầu tính chiều cao và thể tích của hình trụ biết rằng một hình trụ có chu vi đáy là 20cm. Đồng thời, diện tích xung quanh của hình trụ là 14cm2.
Bài làm
Ta có chu vi đáy của hình trụ cũng là chu vi của hình tròn = 2rπ = 20 cm.
Tiếp đến, diện tích xung quanh của hình trụ: Sxung quanh = 2πrh= 20 x h = 14
Suy ra, h = 14/20 = 0,7 (cm)
2rπ = 20 => r ~ 3,18 cm
Bên cạnh đó, công thức tính thể tích của hình trụ là: V = π r² x h ~ 219,91 cm³.
Như vậy, chiều cao của hình trụ là 0,7 (cm) và thể tích của hình trụ là 219,91 cm³.
Bài tập 3: Yêu cầu tính diện tích xung quanh, diện tích toàn phần và thể tích hình trụ. Biết rằng một hình trụ có bán kính đáy r = 7cm, chiều cao h là 9cm.
Bài làm
Ta có công thức tính diện tích xung quanh của hình trụ là :
Sxung quanh = 2πrh = 2π.7.9 = 70π
Bên cạnh đó ta có thể tính được diện tích toàn phần của hình trụ qua công thức :
2πrh + 2πr2: Stoàn phần = 70π+2π.52 = 120π.
Áp dụng ngay công thức V= πr2h để tính thể tích khối trụ.= 2π.52.7 = 350π
Bài tập 4: Yêu cầu tính chiều cao của (T) biết rằng hình trụ (T) có diện tích toàn phần là 120π (cm2) và bán kính đáy r bằng 6cm. Yêu cầu tính độ dài đường sinh của hình trụ ( T)biết rằng hình trụ (T) có thể tích bằng 81π (cm3) và đường sinh gấp 3 lần bán kính đáy (r).
Bài làm
Ta có công thức tính diện tích toàn phần là 2πrh + 2πr2. Căn cứ vào dữ kiện đã cho ở đề bài chúng ta dễ dàng tính được như sau:
Stoàn phần = 2π.6.h + 2π.62 = 120π.
⇒ Từ đó ta dễ dàng suy ra được chiều cao của hình trụ (T) là h = 4(cm).
Ta biết rằng bán kính đáy của hình trụ là r. Theo đề bài cho biết, đường sinh gấp 3 lần bán kính đáy và đường sinh của hình trụ bằng chiều cao nên chiều cao của hình trụ sẽ là 3r.
Ta có công thức tính thể tích của hình trụ là πr2 h, thay vào các dữ kiện đã có ta được: V = πr2.3r = 81π ⇒ r = 3.
Tiếp đến ta tính được độ dài của đường sinh là 3 x 3 = 9cm.
Bài tập 5: Nếu tăng bán kính đường tròn đáy (r) lên hai lần thì thể tích khối trụ mới sẽ là bao nhiêu? Biết rằng, khối trụ có thể tích là 24π.
Bài làm
Căn cứ vào dữ kiện đã cho ở đề bài ta có V = πr2h = 24π.
Khi ta tiến hành tăng bán kính đường tròn đáy lên gấp hai lần thì thể tích khối trụ mới sẽ là:
Nếu tăng bán kính đường tròn đáy lên 2 lần thì ta có:
V’= π(2r)2 h = 4πr2h = 4.24π = 96π.
Trên đây là tổng hợp những kiến thức về hình trụ. Hi vọng, qua bài viết này các bạn sẽ nắm chắc kiến thức và dễ dàng vận dụng vào làm bài tập. Cám ơn các bạn đã quan tâm theo dõi.
>> Xem thêm:
