Hình nón là một trong các hình đặc biệt nhất trong không gian ba chiều. Vì sao họ lại nói hình nón là hình đặc biệt nhất? Nó đặc biệt ở chỗ nào? Cách tính diện tích hình nón ra sao? Hãy tham khảo ngay bài viết của https://vietnamblackberry.vn/ để biết thêm thông tin nhé.
1. Hình nón là gì?
a. Khái niệm hình nón.
Về mặt toán học cũng chưa đưa ra định nghĩa cụ thể thế nào là hình nón. Dựa vào thực tế có thể đưa ra một số định nghĩa sau về hình nón:
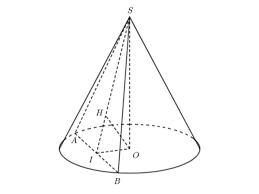
- Hình nón là hình được tạo ra khi quay tam giác vuông một vòng quanh một góc vuông cố định.
- Theo cách hiểu của hình học không gian: hình nón là hình học không gian 03 chiều đặc biệt được tạo ra bởi bề mặt phẳng và bề mặt cong hướng về phía trên. Đầu nhọn của hình nón được gọi là đỉnh, bề mặt phẳng được gọi là đáy.
+ Đồ vật, vật có dạng hình nón trong đời sống như: chiếc nóng là, chiếc mũ sinh nhật, chiếc phễu,…
b. Độ dài đường sinh của hình nón là gì?
- Đường sinh của một hình nón là đường thẳng nối từ đỉnh của hình nón tới trung điểm của cạnh bên. Độ dài đường sinh của một hình nón z có độ dài được tính bằng công thức:
l = √(r^2 + h^2)
Trong đó:
+ r là bán kính đáy của hình nón và h là chiều cao của hình nón.
Ví dụ, nếu bán kính đáy của hình nón là 3m và chiều cao của hình nón là 4m, độ dài đường sinh của hình nón đó sẽ là:
l = √(3^2 + 4^2) = √(9 + 16) = √25 = 5m
Vậy, độ dài đường sinh của hình nón đó là 5m.
2. Cách xác định đơn vị đo hình nón và kí hiệu.
- Để xác định các đơn vị đo lường và ký hiệu của hình nón, chúng ta cần quan tâm đến các kích thước của hình nón đó, bao gồm đường kính đáy, chiều cao và bán kính đáy. Sau đây là các đơn vị đo lường và ký hiệu thường được sử dụng để miêu tả các kích thước của hình nón:
+ Đường kính đáy: Đường kính đáy của hình nón được đo bằng đơn vị đo chiều dài như mét (m) hoặc feet (ft). Ký hiệu thường được sử dụng là “d”.
+ Bán kính đáy: Bán kính đáy của hình nón được đo bằng đơn vị đo chiều dài như mét (m) hoặc feet (ft). Ký hiệu thường được sử dụng là “r”.
+ Chiều cao: Chiều cao của hình nón được đo bằng đơn vị đo chiều dài như mét (m) hoặc feet (ft). Ký hiệu thường được sử dụng là “h”.
+ Diện tích đáy: Diện tích đáy của hình nón được đo bằng đơn vị đo diện tích như mét vuông (m2) hoặc feet vuông (ft2). Ký hiệu thường được sử dụng là “A”.
+ Thể tích: Thể tích của hình nón được đo bằng đơn vị đo thể tích như mét khối (m3) hoặc feet khối (ft3). Ký hiệu thường được sử dụng là “V”.
Các ký hiệu này được sử dụng phổ biến trong các bài toán và công thức tính toán liên quan đến hình nón.
3. Công thức tính diện tích hình nón.
a. Công thức tính diện tích xung quanh hình nón.
Khái niệm diện tích xung quanh.
- Diện tích xung quanh hình nón chỉ bao gồm diện tích mặt xung quanh, bao quanh hình nón, không gồm diện tích đáy.
Công thức tính diện tích xung quanh hình nón.
Công thức tính diện tích xung quanh hình nón được tính như sau:
Sxung quanh = π.r.l
Trong đó:
+ Sxung quanh là diện tích xung quanh hình nón;
+ r là bán kính đáy hình nón;
+ l là độ dài đường sinh hình nón.
Được biểu diễn bằng lời như sau:
Diện tích xung quanh hình nón bằng tích của Pi (π) nhân với bán kính đáy hình nón nhân với đường sinh hình nón.
Hoặc tính với công thức sau: “Công thức tính diện tích xung quanh bằng một nửa tích của chu vi đường tròn đáy và độ dài đường sinh”. Bởi lẽ, π.r chính là nửa chu vi đường tròn.
b. Công thức tính diện tích toàn phần hình nón.
Khái niệm diện tích toàn phần hình nón.
- Diện tích toàn phần của hình nón được tính là độ lớn của toàn bộ không gian hình chiếm giữ, bao gồm cả diện tích xung quanh và diện tích đáy tròn. Hay công thức tính diện tích toàn phần bằng diện tích xung quanh cộng với diện tích của đáy.
Công thức tính diện tích toàn phần hình nón.
Cụ thể như sau:
Stoàn phần = Sxung quanh + Sđáy = π.r.l + π.r2
4. Bài tập tính diện tích hình nón.
Bài tập 1: Cho biết diện tích toàn phần hình nón là 375 cm. Nếu đường sinh của nó gấp bốn lần bán kính, thì đường kính cơ sở của hình nón là bao nhiêu? Sử dụng π = 3
Bài làm
Theo đề bài: l = 4r và π = 3
Diện tích toàn phần hình nón là 375 cm2 nên ta có: 3 × r × 4 r + 3 × r2 = 375
<=> 12r2 + 3r2 = 375
<=> 15r2 = 375
=> r = 5
Vậy bán kính mặt đáy hình nón là 5 => Đường kính mặt nón là 5.2 = 10 cm.
Bài tập 2 : Một hình nón có bán kính 3cm và chiều cao 5cm, tìm diện tích xung quanh của hình nón.
Bài làm
Đề bài đã cho biết bán kính và chiều cao hình nón, tuy nhiên để tính được diện tích xung quanh hình nón ta cần tìm độ dài đường sinh.
Độ dài đường sinh bằng tổng bình phương độ dài đường cao cộng với bình phương bán kính. Hay nói cách khác ta áp dụng định lý pitago để tìm giá trị đường sinh trong hình nón bất kỳ. Ta sẽ tìm được l = 5.83 cm
Áp dụng công thức diện tích xung quanh hình nón đã đề cập ở trên ta có:
Sxung quanh = π.r.l = π.3.5,83 = 54,95 cm2
Bài 3: Cho biết diện tích toàn phần hình nón là 375 cm. Nếu đường sinh của nó gấp bốn lần bán kính, thì đường kính cơ sở của hình nón là bao nhiêu? Sử dụng π = 3
Bài làm
Theo đề bài: l = 4r và π = 3
Diện tích toàn phần hình nón là 375 cm2 nên ta có: 3 × r × 4 r + 3 × r2 = 375
<=> 12r2 + 3r2 = 375
<=> 15r2 = 375
=> r = 5
Vậy bán kính mặt đáy hình nón là 5 => Đường kính mặt nón là 5.2 = 10 cm.
Trên đây là các kiến thức quan trọng về hình nón mà chúng tôi tổng hợp được. Hãy áp dụng đúng công thức để làm bài tập nhé các bạn.
>> Xem thêm:
