Đường trung tuyến là gì? Tính chất, công thức tính đường trung tuyến và bài tập minh họa là câu hỏi mà chúng tôi nhận được nhiều nhất trong thời gian vừa qua. Hôm nay, hãy cùng https://vietnamblackberry.vn/ đi tìm câu trả lời qua bài viết này nhé.

1. Đường trung tuyến là gì? Tính chất của đường trung tuyến.
a. Định nghĩa về đường trung tuyến.
- Đường trung tuyến của đoạn thẳng là một đường thẳng đi qua trung điểm của đoạn thẳng đó.
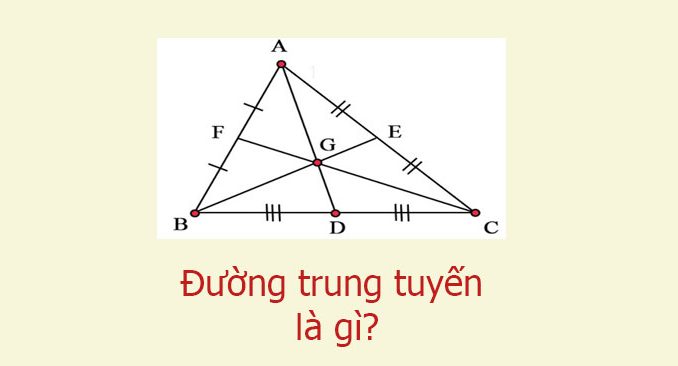
- Đường trung tuyến trong tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.
- Mỗi tam giác sẽ có 3 đường trung tuyến.
- Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau.
b. Tính chất của đường trung tuyến.
- Ba đường trung tuyến của một tam giác cùng đồng quy tại một điểm, điểm này được gọi là trọng tâm của tam giác.
- Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.
- Tam giác vuông là một tam giác đặc biệt với một góc lớn 90 °C, hai cạnh tạo nên góc vuông này luôn vuông góc với nhau, do vậy mà đường trung tuyến của tam giác vuông sẽ mang những tính chát của đường trung tuyến tam giác.
- Trong một tam giác bất kì, đường trung tuyến ứng với cạnh huyền của tam giác sẽ có độ dài bằng 1/2 cạnh huyền.
- Mỗi trung tuyến chia diện tích tam giác thành hai phần bằng nhau. Ba trung truyến chia tam giác thành sau tam giác nhỏ với diện tích bằng nhau.
– Đường trung tuyến trong tam giác cân
- Đường trung tuyến ứng với cạnh đáy thì vuông góc với cạnh đáy. Và chia tam giác thành hai tam giác bằng nhau.
– Đường trung tuyến trong tam giác đều
- Ba đường trung truyến của tam giác đều sẽ chia tam giác đó thành sáu tam giác có diện tích bằng nhau.
- Trong tam giác đều đường thẳng đi qua một đỉnh bất kì và đi qua trọng tâm của tam giác sẽ chia tam giác đó thành hai tam giác có diện tích bằng nhau.
-Đường trung tuyến trong tam giác vuông.
- Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền.
- Một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
- Đường trung tuyến của tam giác vuông có đầy đủ các tính chất của một đường trung tuyến tam giác.
c. Công thức tính đường trung tuyến trong tam giác.
- Độ dài đường trung tuyến của một tam giác được tính thông qua độ dài các cạnh của tam giác và được tính bằng định lý Apollonnius.
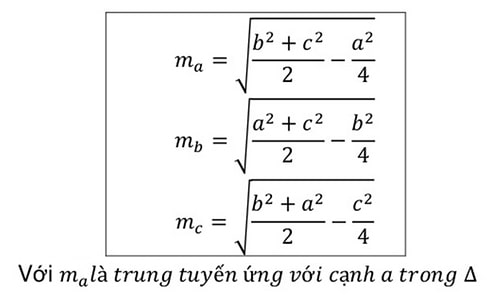
Trong đó:
+ a, b, c: là các cạnh của tam giác.
+ ma, mb, mc: là các đường trung tuyến của tam giác.
2. Bài tập minh họa.
Bài tập 1: Cho tam giác MNP cân ở M có MB = MC = 17cm, NP= 16cm. Kẻ trung tuyến MI.
a) Chứng minh: MI ⊥ NP;
b) Tính độ dài MI.
Bài làm
a. Do MI là đường trung tuyến MNP
=> IP = IN
Mặt khác tam giác MNP cân tại M
=> MI vừa là đường trung tuyến vừa là đường cao
=> MI ⊥ NP
b. Ta có:
NP = 16cm nên NI = PI = 8cm
MN = MP = 17cm
Xét tam giác MIP vuông tại I
Áp dụng Định lý Pitago, ta có:
MP2 = MI2 + IP2
=> 192= MI2 + 82
=> MI2 = 172 – 82 = 225
=> MI = 15cm.
Bài tập 2:
Cho tam giác MNK có MK = MN. Gọi E là giao điểm của hai đường trung tuyến NI và KP. Hãy chứng minh:
a)Tam giác NIK và tam giác KPN bằng nhau
b) EN = EK
c) NK < 4EP
Bài làm:
a) Ta có: MK=MN
NI là đường trung tuyến của tam giác MNK
=> NI = ½ MN (1)
KP là đường trung tuyến của tam giác MNK
=> KP = ½ MK (2)
Từ (1), (2) => NI=KP
Xét tam giác NIK và tam giác KPN, ta có:
NK là cạnh chung
NI = KP
góc KNP = góc NKI (tam giác MNK cân tại M)
=> ΔNIK = ΔKPN (cạnh – góc – cạnh)
b) Ta có:
góc INK= góc PKN (Vì ΔNIK = ΔKPN)
Nên tam giác ENK cân tại E
Suy ra EN = EK
c) Xét ΔMNK ta có:
IM = IK (NI là đường trung tuyến)
PM = PN (KP là đường trung tuyến)
Suy ra IP là đường trung bình của tam giác MNK
=> IP = NK/2
Xét tam giác IPE có
IP < PE + EI (bất đẳng thức Cauchy)
PE = PK – EK
=> NK/2 < PK – EK + EI (3)
ΔNIK = ΔKPN => KP = NI (4)
Tam giác ENK cân tại E => EN = EK (5)
Từ (3), (4), (5) => NK/2 < NI – NE + EP
=> NK/2 < 2EP
=> NK < 4EP
Trên đây là bài viết “Đường trung tuyến là gì? Tính chất của đường trung tuyến và bài tập minh họa” mà đội ngũ thầy cô giáo của chúng tôi muốn gửi đến các bạn. Hi vọng qua bài viết này các bạn sẽ có thêm kiến thức để giải bài tập một cách đơn giản nhất.
>> Xem thêm
