Như các bạn đã biết, định lý Pytago trong chương trình toán học lớp 7 là một kiến thức vô cùng quan trọng. Nó giúp các bạn học sinh giải quyết các bài tập sau này. Hãy cùng https://vietnamblackberry.vn/ tìm hiểu rõ hơn về định lý này qua bài viết “Định lý Pytago là gì? Công thức và bài tập minh họa dễ hiểu” nhé.
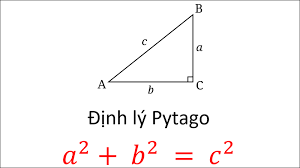
1. Định lý Pytago là gì?
- Mối liên hệ giữa các cạnh trong tam giác vuông đã được con người phát hiện từ thời cổ đại, trước cả Pytago, từ văn minh Ai Cập tới vùng Lưỡng Hà, văn minh Ấn Hằng tới văn minh Trung Hoa cổ đại. Tuy nhiên phải tới thời kỳ của nhà toán học Pytago tức thời Hy Lạp cổ đại, định lý này mới được chứng minh và áp dụng rộng rãi trong toán học. Không chỉ ứng dụng trong hình học đơn giản, Pytago được ứng dụng phổ biến trong các lĩnh vực toán học như vi phân, tích phân, hình học không gian … Vì vậy, định lý Pytago được coi là một thành tựu thúc đẩy sự phát triển của cả nền toán học.
- Định lý Pytago được áp dụng cho việc tính độ dài các cạnh trong một tam giác vuộng. Đây là một liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông.
- Định lý Pytago thuận phát biểu rằng: Trong một tam giác vuông bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
- Theo chiều ngược lại, định lý Pytago nghịch phát biểu rằng: Một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông.
=> Định lý Pytago dùng để dựng đoạn thẳng vô cước, biểu hiện độ dài của các cạnh của một tam giác vuông mà cả ba độ dài này là những số nguyên dương.
2. Công thức định lý Pytago.
a. Công thức định lý Pytago thuận.
- Định lý Pytago thuận: Trong một tam giác vuông bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh góc vuông.
- Hay: Tổng diện tích của hai hình vuông có cạnh là hai cạnh vuông của tam giác vuông (a và b) bằng diện tích của hình vuông có cạnh là cạnh huyền (c).
Cho tam giác ABC vuông tại A. Có độ dài cạnh AB = a, AC = b, BC = c. Áp dụng định lý Pytago, công thức về mối liên hệ giữa các cạnh trong tam giác được biểu diễn như sau:
Tam giác ABC vuông tại A thì ta có: BC² = AB² + AC²
Trong đó:
BC (c): Độ dài cạnh huyền
AB, AC (a,b): Độ dài 2 cạnh góc vuông
b. Công thức định lý Pytago đảo.
- Định lý Pytago nghịch: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
Tam giác ABC có BC² = AB² + AC² => Góc BAC = 90°
Sử dụng định lý Py-ta-go đảo để nhận biết tam giác vuông
Phương pháp:
- Tính bình phương các độ dài ba cạnh của tam giác
- So sánh bình phương của cạnh lớn nhất với tổng các bình phương của hai cạnh kia
- Nếu hai kết quả bằng nhau thì tam giác đó là tam giác vuông, cạnh lớn nhất là cạnh huyền.
3. Một số bài tập vận dụng.
Cách sử dụng định lý Pytago:
+ Nhập hai độ dài mà bạn có vào công thức. Ví dụ: giả sử bạn biết a = 4, b = 8, và muốn tìm độ dài của cạnh huyền c.
+Sau khi các giá trị được đưa vào công thức, chúng ta có 4²+ 8² = c².
+ Bình phương mỗi số hạng để được 16 + 64 = c².
+ Kết hợp các điều khoản như để có được 80 = c².
+ Lấy căn bậc hai của cả hai vế của phương trình để có được c = 8.94.
Bài tập 1:
Tìm độ dài cạnh huyền của một tam giác vuông biết độ dài hai cạnh góc vuông là 3 cm và 4 cm
Bài làm
Bước 1: Viết công thức
c 2 = a 2 + b 2
Bước 2: Thay các giá trị
c 2 = 3 2 + 4 2
c 2 = 9 + 16
c 2 = 25
c = √25
c = 5
Trả lời: Độ dài của cạnh huyền là 5 cm
Bài tập 2: Tìm độ dài một cạnh của tam giác vuông nếu độ dài cạnh huyền là 10 cm và độ dài cạnh kia là 9 cm
Bài làm
Bước 1: Viết công thức
c 2 = a 2 + b 2
Bước 2: Thay các giá trị
10 2 = 9 2 + b 2
100 = 81 + b 2
Bước 3: Trừ 81 cho cả hai vế
19 = b 2
b = √19
b ≈ 4,36
Trả lời: Chiều dài của cạnh là 4,36 cm.
Trên đây là bài viết “Định lý Pytago là gì? Công thức và bài tập minh họa dễ hiểu“. Mong rằng thông qua bài viết này các bạn có thể vận dụng được định lý Pytago để làm bài tập một cách đơn giản nhất. Chúc các bạn thành công!
> Xem thêm.
