Căn bậc 2 là một trong những kiến thức toán học rất quan trọng trong chương trình Trung học cơ sở. Các em cần nắm vững dạng toán này bởi trong các kì thi hay kiểm ra luôn luôn có mặt dạng bài này. Vì vậy, những thông tin sau đây của chúng tôi rất đáng để các bạn dành thời gian đón đọc. Nào chúng ta cùng nhau bắt đầu tìm hiểu nhé.
1. Căn bậc 2 là gì?
a. Khái niệm.
Căn bậc 2 của một số a không âm là số x sao cho x2 = a.
– Căn bậc 2 của a kí hiệu là: 
Ví dụ: Tìm căn bậc 2 của 16.
Vì 42 = 16 và (-4)2 = 16 nên 4 và -4 là hai căn bậc 2 của 16
b. Tính chất của căn bậc 2.
- Mọi số thực a không âm đều có một căn bậc hai không âm duy nhất.
- Mọi số dương a đều có hai căn bậc hai: là căn bậc bai dương 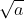và – 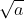là căn bậc hai âm.
- Đối với số dương, căn bậc hai cũng có thể viết dưới dạng kí hiệu lúy thừa
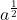
– Hàm số căn bậc hai f ( x ) =
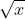( thường là hàm căn bậc hai ) là một hàm số vạch ra tập hợp các số không âm. Căn bậc hai của x là số hữu tỉ khi và chỉ khi z là số hữu tỉ và có thể biểu diễn dưới dạng tỉ số căn bậc hai của hai số chính phương.
2. Cách tính căn bậc 2 và bài tập minh họa.
a. Những phép tính căn bậc 2 cơ bản.
- Một số số bình phương cơ bản và thường thấy nhất để khi khai căn bậc hai, bạn có thể tính nhẩm nhanh hơn:
0² = 0
1² = 1
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289.
Công thức tính căn bậc 2 cơ bản.
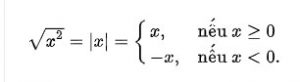
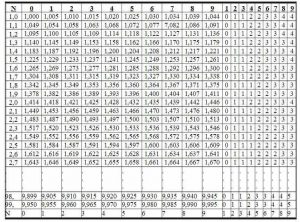
Bảng căn bậc 2.
- Bảng căn bậc hai được chia thành các hàng và các cột, cho phép tìm trực tiếp căn bậc hai của số lớn hơn 1 và nhỏ hơn 100.
- Căn bậc hai của các số được viết bởi không quá ba chữ số từ 1,00 đến 99,9 được ghi sẵn trong bảng ở các cột từ cột 0 đến cột 9. Tiếp đó là chín cột hiệu chính được dùng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn chữ số từ 1,000 đến 99,99.
b. Cách tính căn bậc 2 không cần dùng máy tính.
- Tìm căn bậc hai của số nguyên.
+ Tìm căn bậc hai bằng cách nhân.
– Căn bậc hai của một số là số mà khi bạn nhân số ấy với chính nó, bạn sẽ tìm được số đầu tiên bạn đang có.
– Như vậy có nghĩa là “Bạn có thể nhân số nào với chính nó để ra được số bạn đã có?”
Ví dụ:
Căn bậc hai của 1 là 1 bởi vì 1 nhân 1 bằng 1 (1 X 1 = 1).
Căn bậc hai của 4 là 2 bởi vì 2 nhân 2 bằng 4 (2 X 2 = 4).
Căn bậc hai của 9 là 3 bởi 3 x 3 = 9.
+ Dùng phép chia để tìm căn bậc hai.
– Để tìm căn bậc hai của một số nguyên, bạn có thể lần lượt chia số nguyên ấy với các số cho đến khi bạn tìm được một thương mà giống y hệt số chia của bạn.
Ví dụ:
16 chia 4 bằng 4 nên 4 là căn bậc hai của 16.
4 chia 2 bằng 2, nên 2 là căn bậc hai của 4.
+ Tìm căn bậc hai của các số khác.
– Đoán rồi sử dụng phương pháp loại trừ
Ví dụ:
Tìm căn bậc hai của 20.
Trong khi đó, ta đã biết 16 là một số chính phương với căn bậc hai là 4 (4X4=16).
25 cũng có căn bậc hai là 5 (5X5=25).
Vì vậy, ta sẽ đoán được rằng căn bậc hai của 20 sẽ ở trong khoảng từ 4 đến 5.
2. Bài tập minh họa.
Bài 1: Rút gọn biểu thức A
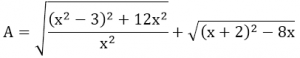
Bài làm
ĐKXĐ: x ≠ 0
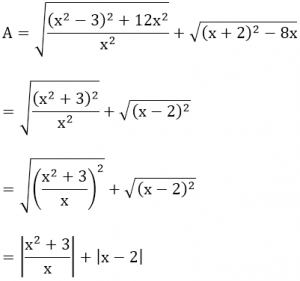
Với x ≥ 2, A trở thành:
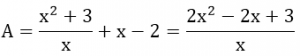
Với 0 < x < 2, A trở thành:
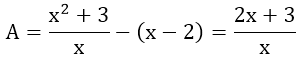
Với x < 0, A trở thành:
Vậy:
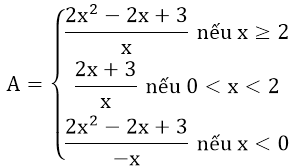
Bài 2: Cho biểu thức: 
a) Rút gọn biểu thức M;
b) Tìm các giá trị của x để M = 4.
Bài làm
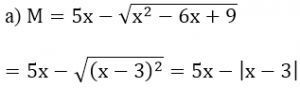
Nếu x ≥ 3 thì M = 5x – (x – 3) = 4x + 3
Nếu x < 3 thì M = 5x + (x – 3) = 6x – 3
b) Ta xét 2 trường hợp
+ M = 4 ⇔ 4x + 3 = 4 ⇔ x = 1/4 (không thỏa mãn x ≥ 3)
+ M = 4 ⇔ 6x – 3 = 4 ⇔ x = 7/6 (thỏa mãn x < 3)
Bài 3: Số nào sau đây là căn bậc hai số học của số a =0.36
A. -0.6
B.0.6
C.0.9
D.-0.18
Bài 4: Số nào sau đây là căn bậc hai số học của số a =2.25
A.-1.5 và 1.5
B.1.25
C.1.5
D.-1.5
Bài 5: Căn bậc hai số học của 9 là
A. 3
B. -3
C.81
D. cả A và B
Bài 6: Câu nào sau đây đúng nhất?
Căn bậc hai số học của 16 bằng
A. 4
B. -4
C. 4 hoặc -4
D. 4 và -4
Bài 7: trong một căn thức:
A.dưới một dấu căn có thể chứa số hoặc chỉ chứa chữ, không thể đồng thời chứa cả hai loại
B. dưới một dấu căn chỉ có thể chứa các căn thức khác
C. dưới một dấu căn chỉ có thể chứa một phân số
D. cả ba câu trên đều sai
E. dưới một dấu căn có thể chứa số, chứa chữ, hoặc có thể chứa cả những dấu căn khác, cùng với các phép tính số học.
Bài 8: Cho số a< . Câu nào sau đây là câu sai?
A. căn bậc hai của a là căn bậc hai số học của số không âm a
B. số a có căn bbậchai lớn hơn 0 và nhỏ hơn 0
C. một trong hai câu A và B là câu sai
D. có ít nhất một trong hai câu A và B là câu đúng
Bài 9: Khẳng định nào sau đây là đúng?
A. căn bậc hai của 121 là 11
B. căn bậc hai của 144 là 12
C. căn bậc hai của 169 là 13 và -13
D. căn bậc hai của 144 là -12
Trên đây là bài viết của https://vietnamblackberry.vn/ về căn bậc 2 là gì? Cách tính căn bậc 2 chuẩn nhất và bài tập minh họa. Hi vọng bài viết của chúng tôi có thể giúp các bạn học sinh hiểu thêm về căn bậc 2. Từ đó, giúp các em có thể giải quyết các bài tập dễ dàng hơn.
> Xem thêm: