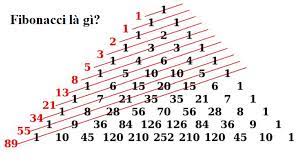
Đã bao giờ các bạn đặt ra câu hỏi Fibonacci là gì chưa? Bạn đã thực sự hiểu về dãy số Fibonacci. Hãy cùng chúng tôi đi tìm hiểu rõ hơn về dãy số Fibonacci qua bài viết dưới đây nhé.
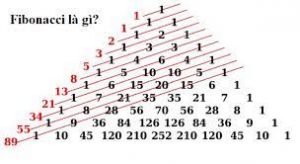
1. Dãy số Fibonacci là gì?
a. Khái niệm về dãy số Fibonacci.
- Dãy Fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng hai phần tử 0 và 1 hoặc 1 và 1, các phần tử sau đó được thiết lập theo quy tắc mỗi phần tử luôn bằng tổng hai phần tử trước nó. Dãy số có quy luật khá đơn giản: “Phần tử đứng sau bằng tổng hai phần tử trước đó cộng lại”. Nghe có vẻ khá đơn giản nhưng nó lại thể hiện rất rõ ràng quy luật phát triển và vận động của vạn vật trong tự nhiên cũng như vũ trụ.
- Có thể nói rằng sự phát triển của dãy số cũng chính là sự phát triển của tự nhiên và có thể giúp chúng ta hiểu thêm về thế giới tự nhiên thông qua Toán học – một sự liên hệ tuyệt vời giữa thực tế và lý thuyết. Chính điều này đã làm nên sự nổi tiếng của dãy số và được coi như là sự hiện diện của tạo hóa ngay bên cạnh con người.
b. Tỷ lệ vàng.
- Từ dãy số Fibonacci chúng ta có thể suy ra một tỷ lệ hoàn hảo gọi là “tỷ lệ vàng” – một tỷ lệ đẹp không tỳ vết. Nó là sự thống nhất hài hòa và không thể đẹp hơn giữa khoa học với nghệ thuật.
- Nếu chúng ta lấy tỉ số của 2 số liên tiếp trong dãy Fibonacci thì sẽ được dãy số sau:
1/1 = 1 2/1 = 2 3/2 = 1,5 5/3 = 1,666… 8/5 = 1,6 13/8 = 1,625 21/13 = 1,61538…
- Tỉ số này sẽ tiến dần đến một giá trị mà ta hay gọi là Tỉ lệ Thần thánh: Ф ≈ 1,618. Một con số liên quan chặt chẽ với Ф là 1/Ф ≈ 0,618. Nghịch đảo của Ф nhỏ hơn nó đúng 1 đơn vị.
- Tỉ lệ vàng Ф có thể quan sát thấy ở vạn vật trong vũ trụ, từ vi mô nhất cho tới vĩ mô nhất, từ các nguyên tử cho tới các dải thiên hà, từ động vật tới thực vật và khoáng vật.
- Trong nghệ thuật tỉ lệ vàng thể hiện rõ ràng trong “hình chữ nhật vàng”, đó là một hình chữ nhật có tỷ số giữa cạnh dài và cạnh ngắn là tỷ số vàng.
2. Các bài toán liên quan đến Fibonacci.
Leonardo Fibonacci là nhà toán học người Ý, được một số người xem là “nhà toán học tài ba nhất thời Trung cổ”. Tên tuổi của ông gắn liền với dãy Fibonacci.
Dãy số Fibonacci công bố vào năm 1202 trong cuốn sách Liber Abacci, được tìm ra qua 2 bài toán kinh điển: bài toán con thỏ và bài toán số “cụ tổ” của một con ong đực.
Bài toán thứ nhất đưa ra giả thiết các đôi thỏ nếu đủ 2 tháng tuổi thì sau mỗi tháng sẽ đẻ được một đôi thỏ con (giả sử các đôi thỏ luôn gồm 2 con đực và cái và không chết). Từ một đôi thỏ sơ sinh ở tháng đầu tiên, Finonnaci muốn tính số thỏ có được ở 1 tháng bất kỳ.
Sau khi thống kê, Fibonacci nhận thấy tháng thứ 1 và tháng 2 chỉ có 1 đôi thỏ. Tháng thứ 3 có 2 đôi, tháng thứ 4 có 3 đôi, tháng 5 có 5 đôi, và cứ thế, số thỏ tháng sau sẽ bằng tổng số thỏ của 2 tháng trước cộng lại.
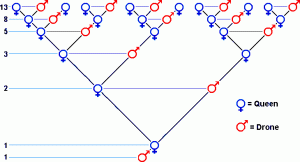
Bài toán thứ hai yêu cầu tìm số tổ tiên của loài ong đực. Nhiều người chỉ biết đến Fibonacci qua bài toán con thỏ, nhưng thật ra còn bài toán về nguồn gốc của ong đực.
Trong sinh học, ong nếu được thụ tinh – tức có cả bố và mẹ, sẽ thành ong cái, ngược lại sẽ là ong đực.
Khi đi tìm nguồn gốc của ong đực, Fibonacci nhận thấy: nếu bắt đầu với 1 con ong đực thì thế hệ trước của nó là 1 con ong cái. Thế hệ trước con ong cái này là 2 con ong gồm 1 đực, 1 cái. Thế hệ trước đó nữa sẽ bao gồm 3 con ong gồm 1 ong cái (sinh ra ong đực) và 2 ong đực và cái (sinh ra ong cái).
Cứ thế tính tiếp tục ta cũng sẽ được dãy 1, 1, 2, 3, 5, 8, 13, 21, 55…
Một số sự kì diệu trong tự nhiên liên quan đến Fibonacci.

- Nếu quan sát các ‘mắt’ trên vỏ của một trái khóm chúng ta cũng thường thấy được số mắt trên 2 đường vòng cung chéo trên vỏ trái thơm là 2 số Fibonacci nào đó ví dụ như 13 và 21.
- Hầu hết các bông hoa có số cánh hoa là một trong các số: 3, 5, 8, 13, 21, 34, 55 hoặc 89. Ví dụ: Hoa loa kèn có 3 cánh, hoa mao lương vàng có 5 cánh, hoa cải ô rô thường có 8 cánh, hoa cúc vạn thọ có 13 cánh, hoa cúc tây có 21 cánh, hoa cúc thường có 34, hoặc 55 hoặc 89 cánh.
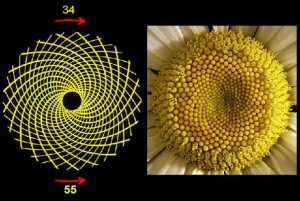
- Các số Fibonacci cũng xuất hiện trong bông hoa hướng dương. Cụ thể trong hoa hướng dương, những nụ nhỏ được xếp thành 2 tập hợp các đường xoắn ốc: một tập cuộn theo chiều kim đồng hồ, một ngược theo chiều kim đồng hồ.
- Số các đường xoắn ốc hướng thuận chiều kim đồng hồ thường là 34 còn ngược chiều kim đồng hồ là 55. Đôi khi các số này là 55 và 89, và thậm chí là 89 và 144. Tất cả các số này đều là các số Fibonacci kế tiếp nhau.
Qua bài viết về Fibonacci các bạn đã thấy sự kì diệu của nó chưa nhỉ. Liệu có phải tất cả chỉ là sự trùng hợp. Hãy theo dõi bài viết của chúng tôi để biết thêm nhiều điều kì diệu nữa nhé.
>>> Xem thêm:
